Серебрянная О.Л., компания Esri CIS, e-mail: oserebryannaya@esri-cis.ru, Web: esri-cis.ru
Regression Analysis for spatial data
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным. Его цель состоит в определении общего вида уравнения регрессии, построении оценок неизвестных параметров, входящих в уравнение регрессии, и проверке статистических гипотез о регрессии. При изучении связи между двумя величинами по результатам наблюдений (x1, y1), …, (xn, yn) в соответствии с теорией регрессии предполагается, что одна из них Y имеет некоторое распределение вероятностей при фиксированном значении х другой.
В приложении к геоинформатике и геоинформационным системам (ГИС) регрессионный анализ позволяет моделировать, исследовать и анализировать пространственные взаимосвязи, а также объяснить факторы, влияющие на эти пространственные взаимоотношения. Регрессионный анализ используется также и для моделирования предположений о возможности осуществления какого-либо (пространственного) события в будущем. Использование инструментов приложения ArcToolbox из набора Моделирование пространственных взаимоотношений (Modeling Spatial Relationships) поможет ответить на такие, например, вопросы, как:
- Почему в некоторых районах люди часто умирают молодыми, чем это может быть вызвано?
- Почему в некоторых местах преступления и пожары происходят значительно чаще, чем в других, и можем ли мы создать модель таких участков, чтобы помочь предотвратить такие события?
- Почему на некоторых участках дорожно-транспортные происшествия происходят значительно чаще, чем на других, есть ли какие-то факторы, напрямую влияющие на это? Можно ли сократить количество ДТП в черте города и/или для конкретных участков дороги путем дополнительного привлечения полицейских или принятия других мер?
Допустим, вы хотите понять, почему в определенном районе люди часто умирают молодыми, или хотите предсказать возможность выпадения ливневого дождя для района, где инструментальные наблюдения за осадками не ведутся или нерегулярны. Инструменты из данного набора предполагают два метода решения таких вопросов: метод наименьших квадратов (МНК, англ. OLS – Ordinary Least Squares) и географически взвешенная регрессия (ГВР, англ. GWR – Geographically Weighted Regression).
МНК, наиболее распространенный метод создания регрессии, является отправной точкой для всех методов пространственного анализа. Он позволяет создать общую модель события, которое вы пытаетесь понять или предсказать (ранние смерти/сильный дождь и др.), и создает одно общее уравнение регрессии для моделирования изучаемого события. ГВР – один из видов пространственного анализа, в последнее время все чаще использующийся для решения аналитических задач в географии и других дисциплинах. Он создает локальную модель переменной или процесса, которые вы хотите предсказать, создавая уравнения для каждого из параметров. При корректном использовании эти методы предоставляют надежный и мощный статистический аппарат для исследования или оценки линейных взаимосвязей.
Линейная взаимосвязь может быть прямой или обратной. Если вы считаете, что при увеличении температуры воздуха увеличивается и количество несчастных случаев, то это положительное взаимоотношение и прямая корреляция. Другой способ описать эту же прямую взаимосвязь – сказать, что количество несчастных случаев уменьшается при снижении температуры воздуха.
И напротив, если вы считаете, что количество преступлений уменьшается при увеличении числа полицейских, которые патрулируют эту территорию, взаимосвязь обратная. Можно описать эту обратную взаимосвязь и так – количество преступлений увеличивается при уменьшении числа полицейских, патрулирующих данную территорию. На иллюстрации, приведенной на рис. 1, видно, что, помимо прямой и обратной взаимосвязи, значимой корреляции может и не быть совсем.
Корреляционный анализ и графики взаимосвязи явлений показывают, насколько сильно два явления зависят друг от друга. Регрессионный анализ, в свою очередь, позволяет получить еще больше информации о взаимосвязи явлений. Этот анализ позволяет показать степень (влияние), с которой одна или несколько переменных могут потенциально вызвать положительное или отрицательное изменение другой переменной.
Использование регрессионного анализа
Регрессионный анализ может применяться для решения многих прикладных задач в разных областях. Например, таким образом можно моделировать пожары с целью определения зон наибольшего риска, а также для выявления тех факторов, которые влияют на их возникновение и распространение. Можно создать модель, которая показывает уменьшение вероятности возгорания участка в зависимости от наличия таких факторов, как количество отделов пожарной охраны, время их реагирования или ценность собственности на участке. Если вы считаете, что время реагирования – это главный фактор, определяющий степень риска, вы будете формировать больше отделов пожарной охраны. Если же вы считаете, что главным фактором является недостаточное финансирование пожарной службы, то вам видимо потребуется увеличить размер средств, выделяемых на пожарную службу.
Регрессионный анализ помогает лучше понять причины происходящих явлений, чтобы вы смогли принять более правильное решение, а так же чтобы предотвратить подобные явления на других территориях и в другое время.
Моделирование явления позволяет лучше понять его суть, что может помочь при принятии управленческих решений, выбрать меры, которые наиболее эффективны в данной ситуации. Основной целью является определение количественной характеристики, которая описывает, как изменения, происходящие в одном или нескольких событиях, влияют на другое событие. Например, при описании основных характеристик местообитаний вымирающих видов птиц следует учесть количество выпадающих осадков, источники пищи, растительность, наличие хищников и др. Определение степени влияния этих факторов на жизнь птиц сможет помочь в создании законодательных документов и принятии других мер, которые будут более эффективно защищать этот вид.
Моделирование явления на основе имеющихся о нем данных для составления прогноза на другие территории или на их состояние в будущем – еще один вариант использования регрессионного анализа. В этом случае главной целью является построение последовательной и точной модели предположения. Вы могли бы использовать такую модель, например, для предсказания выпадения ливней на территориях, где не проводятся инструментальные измерения, основываясь на тех данных, которые у Вас имеются для других территорий, где такие измерения проводятся. Регрессионный анализ может быть осуществлен даже в тех случаях, когда интерполяция невозможна из-за недостаточного размера выборки. Также можно использовать регрессионный анализ для проверки гипотез. Предположим, вы создаете модель совершения преступлений в жилом секторе и хотите понять, как они совершаются и какие меры следует предпринять, чтобы предотвратить их появление.
Изначально, у вас наверняка имеются какие-то гипотезы и предположения, которые надо проверить. Например, такие:
- Существует ли положительная взаимосвязь между случаями вандализма и кражами в квартирах («теория разбитого окна» указывает на то, что испорченная общественная собственность – граффити, разрушенные объекты и т.д. – «притягивают» иные преступления)?
- Существует ли взаимосвязь между употреблением наркотиков и кражами? Могут ли наркоманы воровать для того, чтобы получать средства для покупки наркотиков?
- Больше ли фактов краж в жилом секторе с высокой долей пожилых людей или женщин?
- Где риск совершения кражи выше – в бедных или богатых кварталах?
При использовании регрессионного анализа можно определить взаимосвязи этих явлений и ответить на поставленные вопросы.
Создание регрессионной модели – это последовательный процесс, который включает поиск эффективных независимых переменных для объяснения тех процессов, которые вы пытаетесь смоделировать или понять. Это управление инструментом регрессии для определения переменных, наиболее эффективных для предсказаний явлений, и, затем, удаление и добавление переменных с целью создания наилучшей модели для построения предположения. Далее, в разделе «Компоненты регрессионного анализа: основные термины и компоненты» более подробно рассказывается о терминах, которые используются в регрессионном анализе.
Проблемы, которые могут возникнуть при использовании регрессионного анализа
Метод наименьших квадратов (МНК) – это простое средство, которое имеет и хорошее теоретическое обоснование, и эффективные практические возможности для объяснения и поиска ошибок. Однако МНК будет надежным и эффективным инструментом только в том случае, если ваши данные и регрессионная модель удовлетворяют всем необходимым для работы этого метода требованиям. В ресурсном центре ArcGIS для ArcGIS Desktop (resources.esri.com/arcgisdesktop) можно прочитать статью «Почему регрессионная модель работает с ошибками» (How Regression Models Go Bad), чтобы получить больше информации по этому вопросу. В ней подробно освещена данная проблема и приведены конкретные примеры возможных ошибок.
Для пространственных данных часто не выполняются требования, необходимые для надлежащего функционирования средств регрессионного анализа, поэтому очень важно дополнительно использовать диагностические инструменты, которые позволят определить, насколько применимо для Ваших данных использование метода регрессионного анализа.
Пространственная регрессия
У пространственных данных есть два свойства, которые усложняют требования для проведения статистического анализа (например, МНК) по сравнению с обычными (непространственными) данными. Впрочем, эти свойства и не делают такой анализ невозможным.
Во-первых, географические данные гораздо чаще, чем непространственные данные, уже автокоррелированы. Это означает, что объекты, расположенные в непосредственной близости друг от друга, обычно более схожи, чем объекты, расположенные в удалении друг от друга.
Из-за этого при использовании обычных (непространственных) методов происходит излишний подсчет (переучет) степени влияния этого фактора.
Во-вторых, для пространственных данных в первую очередь важна именно их география.
Часто самыми важными для модели являются непостоянные процессы; эти процессы протекают по-разному на различных участках. Эти особенности могут быть описаны как территориальные изменения или пространственный дрейф.
Поэтому были разработаны специальные методы регрессионного анализа, которые акцентированы именно на эти две особенности пространственных данных. Они предназначены для улучшения моделирования взаимоотношений именно таких данных. Одни пространственные регрессионные методы наиболее эффективно учитывают пространственную автокорреляцию, другие – географическое непостоянство явлений. В настоящее время не существует пространственных регрессионных методов, которые были бы эффективны сразу для всех особенностей пространственных данных. Но для верно построенной модели ГВР пространственная автокорреляция обычно не является проблемой.
На первый взгляд может показаться, что отношение к пространственной автокорреляции у человека, который работает с пространственными данными, и у человека, который использует непространственные данные, должно существенно различаться. При использовании непространственных данных автокорреляция кажется бесполезной функцией, которая не улучшает результат корреляции а, наоборот, нарушает основные принципы анализа, которые традиционно используются при работе с непространственными данными. Приходится исключать ее влияние (например, через перевыборку объектов).
Для географа или ГИС-аналитика пространственная автокорреляция является прямым доказательством важности пространственных процессов в работе. Такая информация является обобщающей для всех остальных данных. Исключение пространства удаляет пространственную составляющую из данных – это примерно как услышать только половину рассказа.
Пространственные процессы и взаимоотношения – основная причина, по которой географы так заинтересованы в пространственном анализе данных.
Но для того, чтобы избежать сверхподсчета влияния пространственных факторов в модели, надо определить полный набор переменных, правильно описывающий всю структуру данных, от которых зависит объект исследования. Если вы не сможете найти все эти переменные, то вероятнее всего будете наблюдать статистически существенный остаток автокорреляции в своей модели. Пока эта ошибка не исправлена, нельзя будет доверять полученным результатам. Используйте инструмент пространственной автокорреляции (Spatial Autocorrelation tool) в наборе инструментов Пространственная статистика (Spatial Statistic Toolbox) для проверки результатов на наличие статистически существенного остатка автокорреляции в вашей модели.
Существует, по крайней мере, три метода работы с пространственной автокорреляцией: изменение исходных переменных, разделение пространственных и непространственных переменных, внедрение пространственной автокорреляции в регрессионную модель. Кратко рассмотрим каждый из них.
Изменение исходных переменных приводит к тому, что пространственная автокорреляция исключается из исходных переменных. В то же время это совсем не гарантирует того, что ее нет вообще. Гораздо более вероятно, что автокорреляция продолжает присутствовать для зависимых переменных, а ведь избавиться необходимо именно от автокорреляции для этих переменных. Этот способ подходит для людей, работающих со стандартными (непространственными) данными. В этом случае (для непространственных данных) причиной появления автокорреляции может быть избыточность данных (т.е. осуществленная выборка сделана слишком подробно).
Разделение пространственных и непространственных компонентов для каждой из переменных может проводиться путем использования регрессионного метода пространственного фильтрования. При этом пространственная составляющая удаляется у каждой из исходных переменных, но добавляется обратно в модель в качестве новой переменной.
Включение пространственной автокорреляции в регрессионную модель реализуется при помощи использования пространственных эконометрических методов. Инструмент Пространственного эконометрического регрессионного метода планируется добавить в ArcGIS в следующей версии.
Региональные вариации
При помощи общих моделей, таких как МНК, можно получить уравнения, которые лучше всего описывают взаимосвязи всех компонентов на всей изучаемой территории. В тех случаях, когда эти взаимосвязи постоянны в пределах всей территории исследования, уравнения, написанные по методу регрессионного анализа МНК, хорошо показывают эти зависимости. Но в тех случаях, когда взаимосвязь между компонентами изменяется в пределах изучаемой территории, регрессионное уравнение получается осредненным для всего набора этих взаимосвязей, и если существуют две противоположных взаимосвязи, то такое осредненное уравнение не покажет хорошо ни одну из них.
В тех случаях, когда изучаемые компоненты имеют различные взаимосвязи на разных территориях, общие модели рушатся, если при их использовании не руководствуются здравым смыслом. В идеале, вам пришлось бы определить весь набор переменных для того чтобы вычленить территориальное изменение, которое внесено зависимой переменной. Но если не удастся определить все эти переменные, вы снова столкнетесь с остаточной пространственной автокорреляцией в модели, что приведет к ухудшению среднеквадратической ошибки модели (среднеквадратическая ошибка – это мера точности работы модели, которая изменяется в пределах от 0,0 до 1,0 и при этом 1,0 соответствует наиболее точной работе модели). Таким образом, пока данная ошибка не будет исправлена, модель нельзя считать верной.
В МНК существует как минимум 4 метода работы с территориальным изменением переменных:
- Включение переменной в модель, которая описывает территориальное изменение. Если, например, вы видите, что модель всегда преувеличена для северных территорий и уменьшена для южных, присвойте им, например, коэффициенты 1 и 0, соответственно.
- Используйте методы, в которых учитываются территориальные изменения, такие как ГВР.
- Используйте значения ошибок регрессии для того, чтобы определить, как переменные коэффициенты влияют на нее. В справке ArcGIS Desktop Online есть статья на эту тему: «Интерпретация результатов регрессии, выполненной с помощью МНК (Interpreting OLS regression results)». Также рекомендуется использовать инструмент ГВР.
- Измените размер области исследования, для того чтобы все взаимосвязи на новых участках исследования были постоянны и не давали территориального отклонения.
Заключительные соображения
Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных. Основная цель заключается в попытке объяснения зависимых переменных, которые вы пытаетесь смоделировать или понять, запуская инструмент регрессии, и определения того, какие величины являются эффективными предсказателями. Затем следует методично удалять и/или добавлять переменные до тех пор, пока вы не найдете наилучшим образом подходящую регрессионную модель. Так как процесс ее создания – занятие творческое, он никогда не должен превращаться в простую «подгонку» данных. Следует учитывать теоретические аспекты, мнение экспертов в этой области и здравый смысл. Вы должны быть способны определить ожидаемую взаимосвязь между каждой потенциальной независимой переменной и зависимой величиной, желательно еще до проведения самого анализа, а если эти связи не совпадают – задавать дополнительные вопросы и находить адекватные решения.
Где еще узнать об использовании этих и других инструментов геостатистики
В данной статье лишь кратко рассказано об инструментах МНК и ГВР, реализованных в ArcGIS Desktop. Esri предлагает множество дополнительных источников для получения информации о регрессионном анализе и о работе инструментов пространственного анализа. Чтобы узнать больше о методах пространственной статистики (и данных инструментах в частности) советуем ознакомиться с веб-справкой ArcGIS Desktop, доступной по адресу resources.esri.com.
Из других полезных и познавательных источников можно упомянуть о книге The Esri Guide to GIS Analysis, Volume 2: Spatial Measurements and Statistics (Путеводитель по ГИС-анализу Esri, издание второе: Пространственные измерения и статистика) Энди Митчелла, в которой рассказывается о том, как правильно строить и эффективно использовать методы пространственного анализа (рис. 2). Есть и другие ресурсы с разными материалами по пространственной статистике и примерами ее эффективного использования, например, имеется специальный блог (см. http://esriurl.com/spatialstats). Можно также посмотреть часовое видео «Пространственная статистика: лучшие примеры» (Spatial Statistics: Best Practices, с текстовой расшифровкой стенограммы, на англ.) по адресу http://video.esri.com/watch/903/spatial-statistics-best-practices. В нем показаны рабочие процессы и детали вариантов пространственного анализа с использованием инструментов регрессии.
Широкие возможности пространственного анализа с использованием статистических и геостатистических методов исследования геоданных, расширяющие стандартные возможности ArcGIS, предоставляют дополнительные модули ArcGIS, прежде всего, – это ArcGIS Spatial Analyst и ArcGIS Geostatistical Analyst.
В основу этой статьи положены материалы с сайта компании Esri.
Компоненты регрессионного анализа: термины и основные понятия
Невозможно в достаточной мере понять и уж тем более использовать средства регрессионного анализа без знания основных терминов и концепций, на которых этот вид анализа основывается. В качестве приложения приведем их краткий перечень.
Уравнение регрессии – это математическая формула, которая применяется для описания исходных переменных. Такое уравнение поможет наилучшим образом предсказать те переменные, которые вы пытаетесь смоделировать. Следует обратить внимание и на то, что X и Y – это не координаты, как в географии, а переменные (зависимые и независимые) величины. Причем зависимая переменная – это всегда y, а независимые переменные всегда x. Каждой независимой переменной соответствует коэффициент регрессии, математически описывающий степень и характер влияния этой переменной на зависимую. Уравнение регрессии должно выглядеть примерно так, как это показано на рисунке 3, здесь y является зависимой переменной, Xs – исходные переменные, βs – коэффициенты регрессии. Предположим, что вам необходимо создать модель кражи в жилом доме (RES_BURG) и предсказывать возможность ее совершения в будущем на исследуемом участке. В качестве определяющих факторов для анализа этого события в данном случае выбраны средние доходы жителей этих домов (MED_INC), количество актов вандализма (VAND) и количество самих домов (HH_UNITS). В таком случае уравнение регрессии будет иметь следующий вид:
RES_BURG = β0 +β1*(MED_INC)+β2*(VAND)+β3*(HH_UNITS)+ε
Зависимая переменная (y) – это переменная, которая описывает моделируемый процесс, например: кража в жилом доме, потеря права выкупа вещей из ломбарда, ливень, пожар и пр. Эта переменная записывается в левой части уравнения регрессии. Несмотря на то, что вы используете это уравнение именно для того, чтобы определить зависимую переменную y, вы наверняка примерно представляете себе те значения, которые она может принимать. И эти значения можно использовать для построения или исправления регрессионной модели. Известные значения y обычно называют наблюдаемыми значениями.
Независимые (исходные) переменные (X) – используются для создания модели или предсказания значений неизвестного параметра y. В уравнении регрессии независимые переменные записываются в правой части. То есть, зависимая переменная – это функция от независимых (исходных) переменных. Если вы хотите, например, определить список и количество товаров для формирования ассортимента продаж в определенном магазине, то необходимо будет включить в модель такие исходные переменные, как количество потенциальных клиентов, а также тот факт, хорошо ли виден магазин издалека, местные предпочтения потребителей в выборе товаров и др. параметры.
Коэффициенты регрессии (β) – вычисляются при помощи использования инструмента регрессии. Эти значения, по одному для каждой из независимых переменных, описывают степень и характер влияния, которое оказывают исходные переменные на зависимую. Предположим, что вы определяете опасность возгорания как функцию от прихода солнечного излучения к земной поверхности, характера растительности, количества выпадающих осадков и экспозиции склона. Скорее всего, получится прямая связь между опасностью возгорания и приходом солнечной энергии, то есть, чем больше солнечного излучения приходит на Землю, тем чаще возможны случаи возгорания для этой территории. Если взаимосвязь прямая, то перед коэффициентом в уравнении ставится знак плюс. И наоборот, взаимосвязь количества выпадающих осадков и числа возгораний будет обратной. В этом случае перед коэффициентом в уравнении ставится знак минус. Если объекты или явления зависят друг от друга очень сильно, то коэффициент перед независимой переменной в уравнении будет большим. Слабая взаимосвязь определяется коэффициентами, близкими к нулю. Β0 – это точка пересечения с осью Y. Этому коэффициенту будет равна зависимая переменная, если все оставшиеся коэффициенты уравнения примут значение ноль.
Достигаемые уровни значимости (p-values) – вычисляются при помощи статистического теста и служат для определения вероятности для каждого из коэффициентов в регрессионном уравнении. Нулевая гипотеза для статистического теста доказывает, что коэффициенты отличаются от нуля незначительно; другими словами, для всех переменных в модели с коэффициентами близкими к нулю взаимосвязи с изучаемым объектом незначительны и не помогут улучшению качества модели. Небольшие значения достигаемого уровня значимости (p-value) показывают, что данная переменная необходима для работы модели, со значимостью, значительно превышающей ноль (коэффициент перед такой переменной не ноль). К примеру, можно сказать, что коэффициент с достигаемым уровнем значимости, равным 0,01, будет статистически важен для модели с вероятностью 99%. Такой коэффициент очень важен для создания вашего предположения. Переменные с близкими к нулю коэффициентами не помогут при построении модели предположения; они практически всегда удаляются из регрессионного уравнения, если нет особых теоретических причин для того чтобы их в нем оставить.
Среднеквадратическая ошибка (R2/R) – изменяется в пределах от 0 до 100%, является мерой качества выполнения регрессионного анализа. Выделяют множественный и скорректированный коэффициенты среднеквадратической ошибки. Если созданная вами модель идеально описывает взаимосвязь явлений, то среднеквадратическая ошибка будет равна нулю. Но скорее всего вы допустили неточности при создании модели (учет сразу всех факторов, влияющих на какое-либо событие, очень маловероятен), если в результате получили такое значение ошибки. Возможно, вы пытались предсказать явление y при помощи того же самого явления y. Чаще всего, вы будете получать ошибку, близкую к 0,49, такая ошибка означает, что ваша модель на 49% верно объясняет взаимосвязь явлений. Чтобы понять, для каких именно значений среднеквадратическая ошибка наиболее велика, постройте гистограмму, показывающую как предположенное вашей моделью значение y, так и то, которое наблюдается в действительности, затем отсортируйте гистограмму по оцениваемым значениям (рис. 4). Отметьте, сколько на этой гистограмме наложений двух параметров y. Такой график позволяет визуально определить, насколько хорошо были предсказаны значения зависимой переменной в данной модели. Скорректированный коэффициент ошибки будет всегда немного меньше, чем множественный, т.к. он показывает всю модель в комплексе.
Остаток (Residual) – это оставшаяся необъясненной зависимость между переменными. В уравнении он представлен как ε – случайная ошибка. Для создания и исправления регрессионной модели используются известные значения определяемой переменной. Если использовать все известные значения переменных Y и X, инструмент регрессии напишет уравнение, которое будет с наибольшей точностью предсказывать новые значения y. Но эти предсказанные значения очень редко будут в точности совпадать с теми, которые происходят в реальности. Разница между предсказанными и случившимися значениями y называется остатком (рис. 5). Величина этого остатка является одной из мер качества созданной модели. Большой остаток указывает на низкую работоспособность модели.
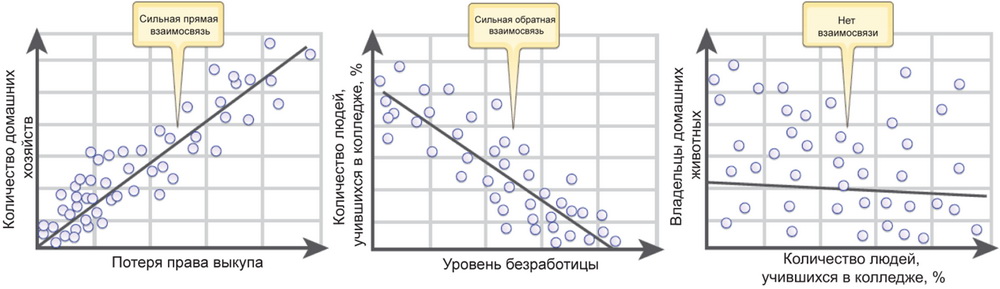 Рис. 1. На этих графиках показаны зависимости между двумя переменным: прямая, обратная и отсутствие зависимости |
 Рис. 2. Изданная Esri Press книга Энди Митчелла «Путеводитель по ГИС-анализу Esri, издание второе: Пространственные измерения и статистика» |
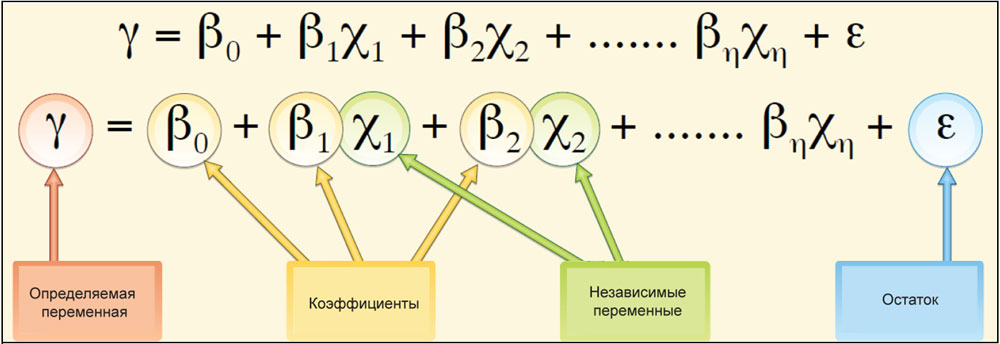 Рис. 3. Элементы регрессионного уравнения |
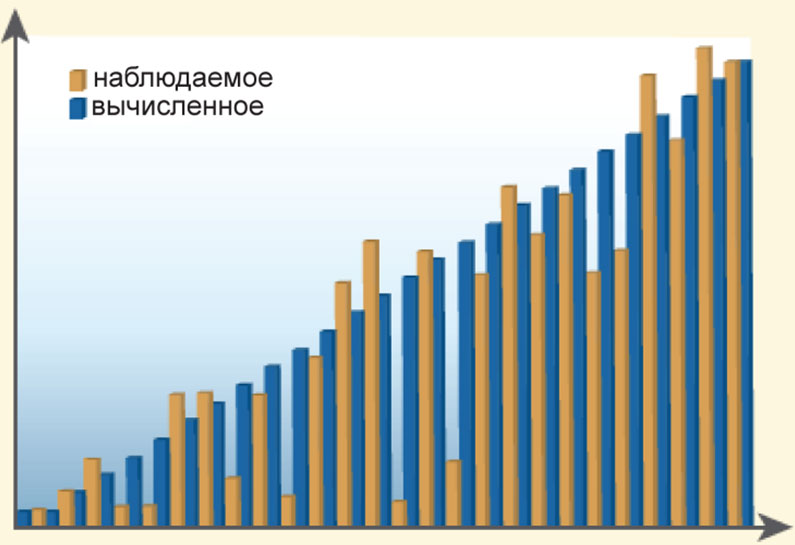 Рис. 4. Среднеквадратическая ошибка – это мера качества модели, показывающая насколько точно наблюдаемые явления соответствуют вычисленным |
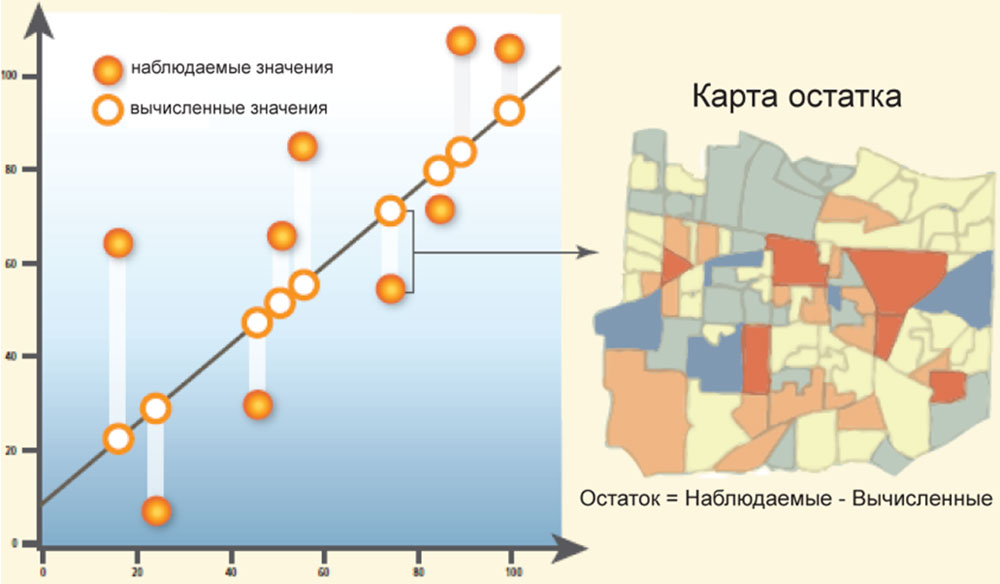 Рис. 5. Регрессионный остаток |