Котиков Ю.Г., д.т.н., профессор кафедры организации перевозок, управления и безопасности на автомобильном транспорте, академик РАТ, Чудаков Р.С., аспирант СПбГАСУ, Санкт-Петербург, E-mail: cotikov@mail.ru
 Функциональное развитие ГИС-инструментария на уровне семейства продуктов ArcGIS 9 открывает новые возможности решения крупномасштабных задач моделирования и анализа данных, проектирования и сопровождения аналитических и управленческих систем в транспортной сфере. Вот далеко не полный перечень таких задач: сетевые задачи распределительной логистики; управление многослойной совокупностью логистических потоков; моделирование транспортного пространства; моделирование транспортных коридоров; транспортные модели мегаполиса; сетевое планирование ресурсов; сетевое моделирование транспортной энергетики; релаксация организации движения на сети под потоком возмущений. Обратимся к первой из этих задач.
Функциональное развитие ГИС-инструментария на уровне семейства продуктов ArcGIS 9 открывает новые возможности решения крупномасштабных задач моделирования и анализа данных, проектирования и сопровождения аналитических и управленческих систем в транспортной сфере. Вот далеко не полный перечень таких задач: сетевые задачи распределительной логистики; управление многослойной совокупностью логистических потоков; моделирование транспортного пространства; моделирование транспортных коридоров; транспортные модели мегаполиса; сетевое планирование ресурсов; сетевое моделирование транспортной энергетики; релаксация организации движения на сети под потоком возмущений. Обратимся к первой из этих задач.
Сетевые задачи распределительной логистики
Размещение логистических мощностей осуществляется по результатам решения задачи определения границ ареала выгодного сбыта для фирмы. При множестве конкурентов анализ множества ареалов должен иметь сетевой и пространственный характер.
Точечные распределения в сетях в простейшем случае могут характеризоваться с помощью полигонов Тиссена, основанных на идее наращивания полигонов вокруг точек для показа их зон влияния во множестве других точек области. Но реальные транспортные сети являются нерегулярными, а сопротивление продвижению транспортных средств – переменно относительно пространственных координат. Поэтому отображение в форме Тиссена может использоваться на ранних стадиях исследования, давая начальное, упрощенное представление о распределении ареалов сбыта в регионе.
До недавнего времени решение транспортных задач осуществлялось схематически с помощью графов, а сетевой и пространственный анализ, по сути дела, не выполнялся.
Другим актуальным аспектом распределительной логистики является рассмотрение инфраструктуры, среды, в которой осуществляется производство распределения.
Важным аспектом также является глобальная эффективность системы распределения – отношение количественных характеристик на выходе и входе распределительной системы. Поясним этот тезис на примере системы топливообеспечения автомобильного транспорта. Ведь процесс обеспечения транспортной перевозки топливом не заканчивается заливкой топлива в бак автомобиля. Доставка топлива до двигателя продолжается и во время движения автомобиля при осуществлении перевозки, а топливный бак является передвижным хранилищем. Учет всего объема топлива, находящегося в баках движущихся автомобилей, а также в емкостях АЗС и узловых хранилищ, несомненно влияет на эффективность работы транспорта в целом. Существование узловых хранилищ также требует оптимизации процесса доставки топлива от них до АЗС.
И становится очевидным, что уж если общая энергоэффективность транспорта должна оцениваться по отношению произведенной транспортной работы к энергии, содержащейся в топливе, расходуемом на совокупный транспортный процесс [1], то энергоэффективность системы топливообеспечения должна оцениваться долей энергозатрат на доставку топлива (от хранилищ до АЗС, от АЗС до баков – путем доставки автомобиля к АЗС, от баков до двигателей – непрерывно в процессе перевозки).
С появлением современного ГИС-инструментария, вкупе с другими ресурсами корпоративной информационной среды, постановка решения таких задач становится вполне правомерной.
Изложенные идеи используются в курсе математического моделирования транспортных систем для студентов транспортных специальностей Санкт-Петербургского государственного архитектурно-строительного университета (СПбГАСУ).
Последовательность решения комплексной задачи распределения автомобильного топлива в регионе
Поделимся практикой моделирования средствами ArcGIS сетевых задач распределительной логистики. Его объектом явилась система обеспечения топливом автотранспорта Санкт-Петербурга. Исследование проводилось в рамках лабораторного практикума студентов Автомобильно-дорожного факультета СПбГАСУ на базе университетской лицензии ArcGIS 9 c Network Analyst и другими дополнительными модулями.
Продвижение в решении задачи было намечено вести в последовательности:
- 1) определение границ рынка на прямой, соединяющей двух конкурентов;
- 2) далее развертка ареалов двух конкурентов на плоскости (в однородной среде);
- 3) переход к ареалам для трех ближайших конкурентов (как элементов TIN’а);
- 4) сеть конкурентов в регионе (пока в однородной среде);
- 5) сеть конкурентов на реальной неоднородной улично-дорожной сети (УДС) региона;
- 6) учет распределения единичных потребителей топлива (отдельно взятых машин);
- 7) экономический анализ на базе проведенного сетевого анализа.
Подготовка картографического материала
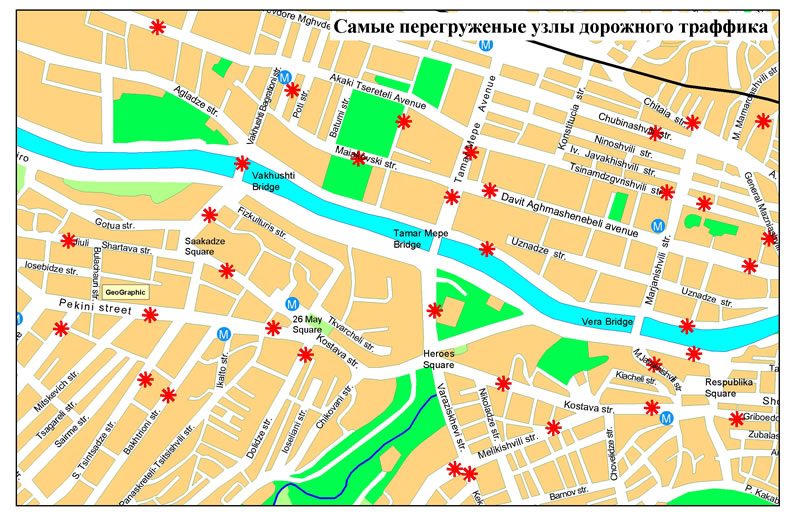
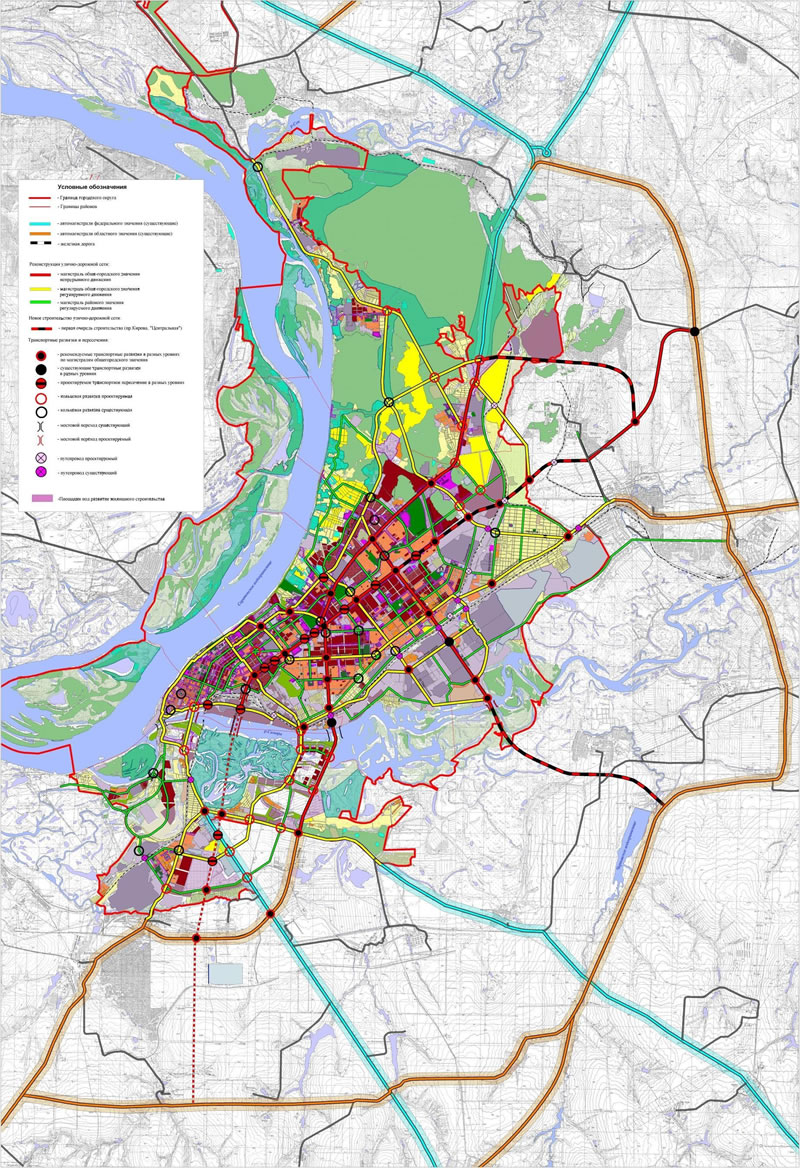
Проведена оцифровка земельных и водных ресурсов, УДС города и сети АЗС. Для Калининского района оцифровка УДС выполнена под требования Network Data Set c учетом ограничений на повороты для всех перекрестков (рис. 1).
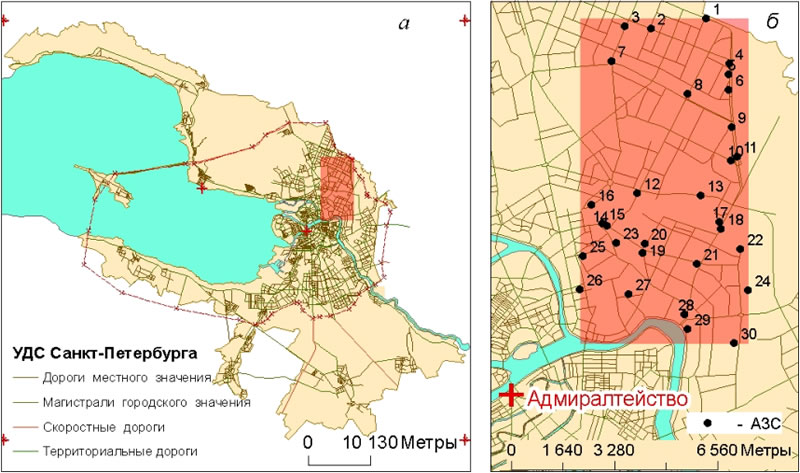
Рис. 1. Улично-дорожная сеть Санкт-Петербурга (а) и ее часть (красный фон), пролегающая в Калининском районе (б).
Использованы следующие системы координат:
- · Географическая система координат: GCS_Pulkovo_1995. Датум: D_Pulkovo_1995.
- · Начальный меридиан: 0. Угловые единицы: Degree.
- · Система координат проекции: Local2. Проекция: Local. False_Easting: 0,00000000.
- · False_Northing: 0,00000000. Scale_Factor: 1,00000000. Azimuth: 0,00000000. Longitude_Of_Center: 30,31000000. Latitude_Of_Center: 59,93750000. Линейные единицы: Meter.
Центр системы координат проекции привязан к Адмиралтейскому шпилю – весьма удобная точка для оцифровки. Опорные точки калибровались по нескольким картам и снимкам различного происхождения. Экстент для полного охвата города составил: -49330 – +25670 м по X; -33820 – +34180 м по Y.
Определение границ рынка на прямой, соединяющей двух конкурентов (в однородной среде)
При расположении фирм А и В на расстоянии L друг от друга границей рынка на соединяющей их прямой будет точка равновыгодности T, где СА = CB [2], т.е.
СрА + СtА xA = СрB + СtB(L – xA), (1)
где Ср – производственные затраты, ден. ед./ед. товара; Сt – транспортный тариф на доставку груза, ден. ед./(ед. товара•км); хА – расстояние от предприятия А до потребителя, км.
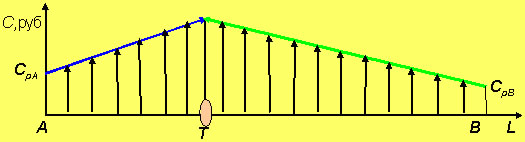
Рис. 2. Зависимость общих затрат предприятий по производству и доставке товара к потребителю.
Затраты по доставке товара в конкретную точку линейно возрастают с удалением потребителя от производителя (рис. 2). Тогда суммарные затраты по линии реализации продукции будут равны интегралу функции затрат по ареалу предприятия:
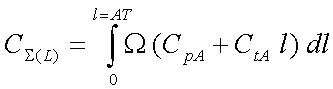 , (2)
, (2)
где ![]() – суммарные затраты по линии влияния, руб.;? – плотность распределения потребителей по линии распределения, потр./км; l – расстояние от предприятия до потребителя, км.
– суммарные затраты по линии влияния, руб.;? – плотность распределения потребителей по линии распределения, потр./км; l – расстояние от предприятия до потребителя, км.
Развертка ареалов двух конкурентов на плоскости (в однородной среде)
На плоскости транспортные расходы предприятий по доставке товара в конкретную точку однородного пространства изменяются пропорционально расстоянию от предприятия до потребителя – в любом из направлений. Линии равных суммарных затрат на единицу продукции (изокосты) являются окружностями (рис. 3) [3, 4].
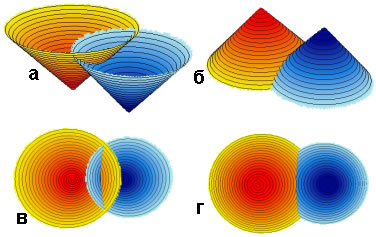
Рис. 3. Представление затрат (а и в) и дохода или прибыли (б и г): 3D – вверху, 2D – внизу.
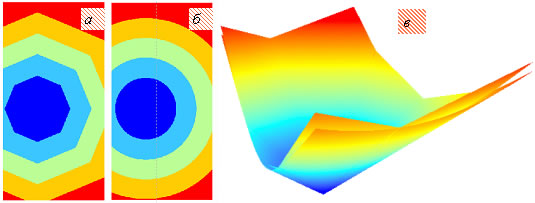
Рис. 4. Сравнение результатов вычисления и отображения растра со стоимостным расстоянием для одного источника (АЗС № 12 при Сp = 0): а) процедурой Spatial Analyst расчета Взвешенного расстояния; б) через расчет растра Прямого расстояния с последующим линейным преобразованием его в Калькуляторе растра; в) отображение двух вариантов в ArcScene.
В 3D-изображении, если ось аппликат Z отвести под общие затраты, то совокупность изокост образует конус с вершиной в концентре с координатами (x0, y0, z0), где x0 и y0 – координаты месторасположения предприятия, а z0 – производственные затраты Ср (рис. 3, а). При этом суммарные затраты для каждого предприятия будут равны объему фигуры, находящейся под его конусом до отметки z =0.
Конусы пересекаются по пространственной кривой, проекция которой на плоскость (x,y) является границей ареалов выгодного сбыта конкурирующих предприятий A и B (см. рис. 3, в и г). Случай неравных производственных затрат конкурентов в полярных координатах (?, ?) описывается формулой:
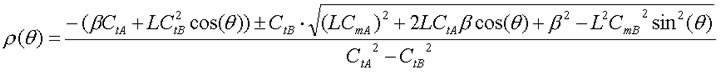 , (3)
, (3)
где ? = СрА — СрB – разность между производственными затратами предприятий [3, 4].
Смена направления шкалы затрат позволяет перевернуть фигуру рис. 3, а «с ног на голову», представляя видом рис. 3, б поверхность «минус затраты» (назовем ее «поверхностью доходов»). Эта поверхность удобна для визуального анализа – линия пересечения между конусами является линией равновыгодности в смысле условия (1). Проецирование изокост на плоскость (x,y) приводит к видам в и г, представляющим собой ареалы выгодного сбыта конкурентов.
Отображение ареалов двух конкурентов (в однородной среде)
Первые попытки расчета стоимостного расстояния в Spatial Analyst (Расстояние/Взвешенная стоимость, а также ArcToolbox/Spatial Analyst Tools/Distance/Cost Distance) привели нас к неудовлетворительному отображению. Это видно на рис. 4, а для одной АЗС. Причина была найдена в алгоритме Cost Distance algorithm (см. Help). Там по схеме расчета растра для конуса по направлениям ? = ?k/4 накапливается погрешность с одним и тем же коэффициентом – так что, в принципе, получается граненая фигура.
Проба расчета по цепочке действий: получение растра прямого расстояния DirDist – затем применение к нему преобразования CostDist = Cp + Ct * [DirDist] (обозначения Cp и Ct см. в формуле (1)), – привела к приемлемому результату – см. рис. 4, б. Разницу по координате Z между результатами, получаемыми двумя способами, можно видеть на рис. 4, в. Исходя из этого, для дальнейшего анализа выбран второй способ.
Для расчета и отображения ареалов выгодного сбыта (Распределений в терминологии ArcGIS), а также построения общей поверхности затрат по региону, разработан следующий алгоритм для работы в Spatial Analyst: 1) для каждого источника рассчитываются индивидуальные стоимостные поверхности; 2) с применением функции min( , , ,) вычисляется растр нижней оболочки множества индивидуальных поверхностей – растр общей стоимостной поверхности региона; 3) с учетом образовавшихся границ смыкания индивидуальных ареалов сбыта строится растр распределений; 4) рассчитается объем фигуры под стоимостной поверхностью региона; 5) полученные результаты отображаются в ArcScene.
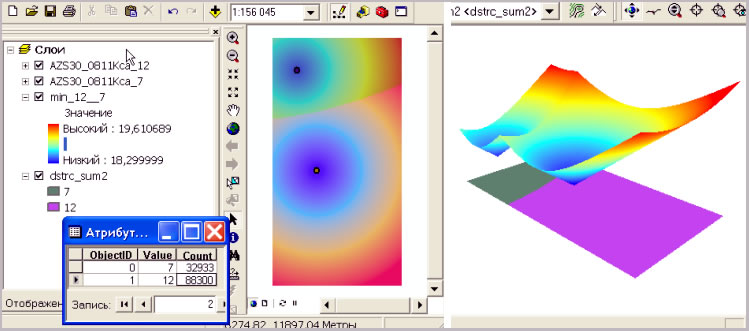
Рис. 5. Стоимостной растр, стоимостная поверхность (с учетом Сp) и ареалы выгодного сбыта для конкурирующих АЗС №№ 7 и 12.
Стоимостной растр, стоимостная поверхность с распределениями для условно конкурирующих АЗС №№ 7 и 12, приведены на рис. 5. В таблице содержания указаны значения суммарных затрат Ср + Сt*? в руб./литр (см. 18,299 – 19,610). Плоскость с распределениями ареалов сбыта здесь и на последующих рисунках помещена на уровне 18 руб./литр.
Ареалы для трех ближайших конкурентов
Рассмотрение совокупности полученных конусов облегчает анализ затрат и доходов предприятий. Примером служит серия кадров, иллюстрирующих влияние транспортного тарифа на затраты предприятия D (рис. 6 – зеленая окраска) – прослеживается тенденция к расширению конуса предприятия D при снижении его тарифа на перевозку. С ростом емкости рынка сбыта растет объем суммарной прибыли (пропорционально объему части конуса, возвышающейся над ареалом сбыта – см. виды а, б, в).
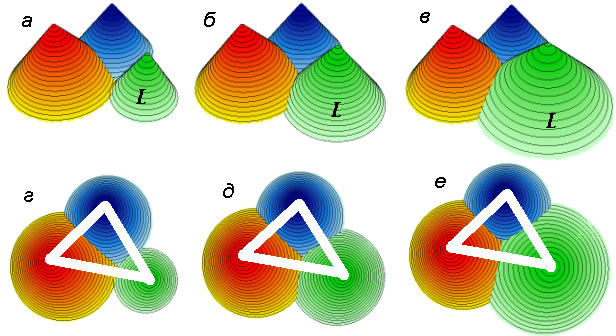
Рис. 6. Кадры анимации отслеживания влияния транспортного тарифа предприятия D на экономическую конъюнктуру.
Проекция сверху на «поверхность доходов» позволяет осуществить привязку к географическим координатам и провести сравнительный анализ ареалов сбыта для конкурентов. На плоскости затраты по ареалу предприятия рассчитываются как двойной интеграл по полярному углу и радиусу [5]:
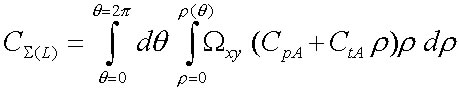 , (4)
, (4)
где ?(?) – граница выгодного сбыта предприятия, описываемая формулой (3); ?xy – плотность распределения потребителей по ареалу как функция от параметров ? и ?, однако с размерностью потр./м2.
Сеть конкурентов в регионе (в однородной среде)
Перебор вариантов триангуляции для сети начинается при наличии минимум трех соседей вокруг. На рис. 7 и 8 отображены результаты моделирования ситуации для конкурирующих АЗС №№ 7, 8, 12, 25 и 28.
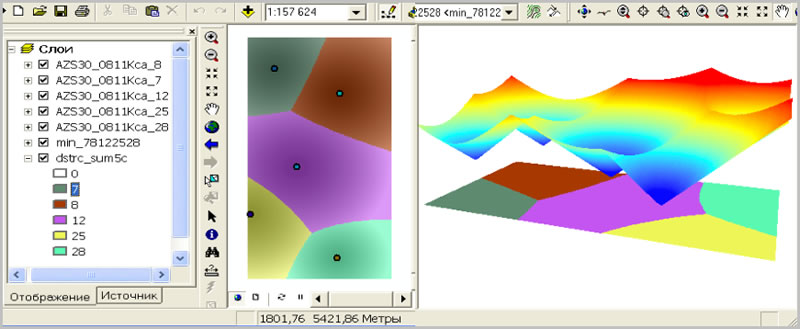
Рис. 7. Стоимостной растр, стоимостная поверхность (с учетом Сp) и ареалы выгодного сбыта для конкурирующих АЗС №№ 7, 8, 12, 25 и 28.
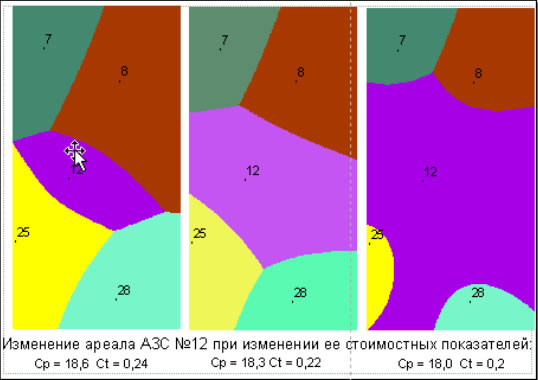
Рис. 8. Экспансия АЗС №12 при снижении ее удельных затрат.
Рассмотрим, насколько может деформироваться прямолинейная топография полигонов Тиссена (когда Cp=const и Ct = const для всех конкурентов) при изменении для отдельных источников как начальной цены Cp, так и транспортного тарифа Ct. Проследим это на примере формирования границ рынка сбыта. Были реализованы ситуации с АЗС №№ 7, 8,12, 25 и 28 (промежуточные АЗС условно выведены), когда менялись Cp и Ctдля центральной АЗС №12, в соответствии с таблицей:
| Параметр |
№ АЗС и вариант |
||||||
|
7 |
8 |
25 |
28 |
12_a |
12_b |
12_c |
|
|
Cp, руб/литр |
18,4 |
18,4 |
18,3 |
18,6 |
18,6 |
18,3 |
18,0 |
|
Ct, руб/(км?литр) |
0,23 |
0,22 |
0,26 |
0,24 |
0,24 |
0,22 |
0,20 |
Результаты моделирования представлены на рис. 8. Видно, например, что граница в паре 28-12_а прямолинейная и находится на равных расстояниях от источников, что соответствует границе по Тиссену. Граница в паре 12_b–8 чуть прогнута в пользу 12_b из-за меньшей величины Cp. В целом кадры анимации дают представление о характере экспансии АЗС №12 при снижении ее затрат. На нескольких последующих рисунках отображены результаты моделирования ситуации в однородной среде для всех 30-ти конкурирующих АЗС Калининского района.
Растр распределения ареалов выгодного сбыта (рис. 9) построен с помощью Spatial Analyst в несколько шагов. На первом этапе с использованием оператора «Расстояние по прямой» определены индивидуальные растры стоимостного расстояния. Суть этого построения заключается в определении Эвклидова расстояния от конкретной АЗС до границ общего экстента (нижний растр на рис. 10). На втором этапе растр стоимостного расстояния с помощью калькулятора растра преобразовывался в стоимостную поверхность – путём добавления коэффициентов отпускной цены топлива Cp(высота столбика на рис. 10) и транспортного тарифа Ct. На следующих этапах с использованием функции минимизации и суммирования строился растр распределения ареалов, представленный на рис. 9. На рис. 11 отображены результаты совместного 3D-моделирования растра распределения ареалов и стоимостной поверхности для 30-ти АЗС в идеальной среде: плоскость с ареалами выгодного сбыта находится на высоте 18 руб./литр.
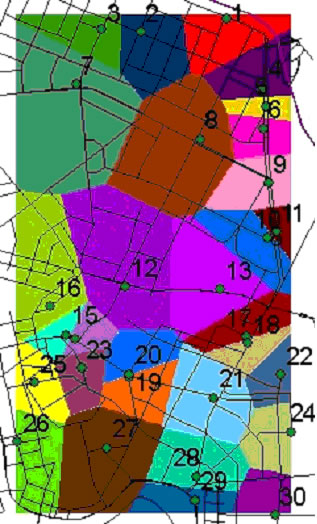
Рис. 9. Растр распределения ареалов 30-ти конкурирующих АЗС (в идеальной среде), наложенный на реальную УДС.
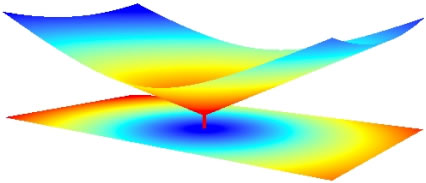
Рис. 10. Отображение растра стоимостного расстояния и стоимостной поверхности.
По рис. 9 видно, что построенный растр никак не коррелирует с реальным расположением дорог – следствие того, что моделировалась ситуация условного размещения предприятий в идеальной однородной среде (без учета топологии УДС). Модель системы топливообеспечения, рассчитанная только по двум параметрам (Cp и Ct), в условиях движения транспорта в мегаполисе не является адекватной. Реальная среда неоднородна по импедансу: расстояния не эвклидовы, функциональные стоимости сопротивления перемещению – переменные, маршруты – криволинейные и т.д.
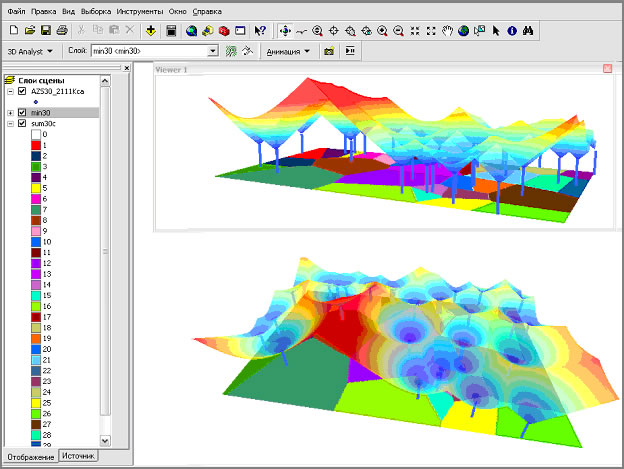
Рис. 11. Стоимостная поверхность (с учетом Сp) для 30-ти конкурирующих АЗС.
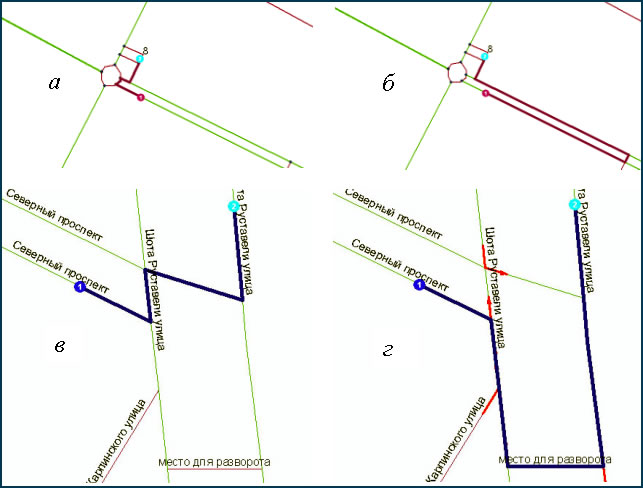
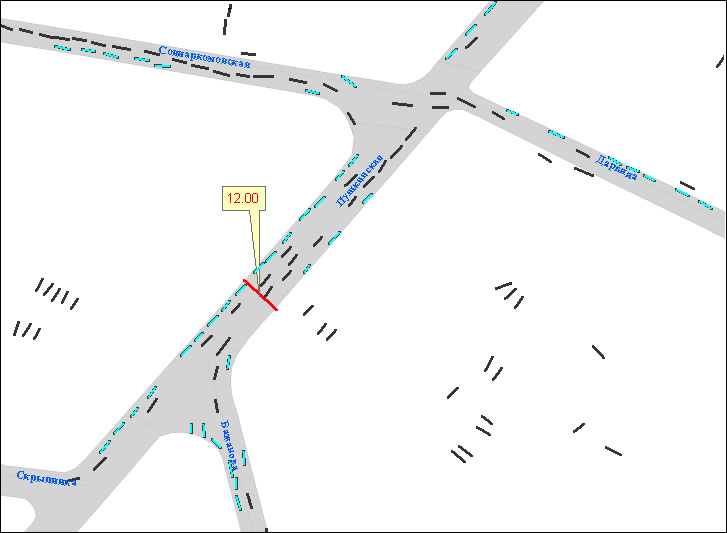
Рис. 12. Движение транспорта по УДС: а и в – условно без ограничений по ПДД; б и г – с ограничениями по ПДД.
С целью повышения степени адекватности моделирования дорожно-транспортной обстановки в городе привлечены функции модуля Network Analyst. Во-первых, были смоделированы положение АЗС и подъезды к ним: точное расположение АЗС на нужной стороне дороги, учёт разрешённых и запрещённых манёвров. Рис. 12 демонстрирует, насколько меняется траектория и увеличивается путь автомобиля к АЗС при организации движения по правилам (рис. 12, б) по сравнению с движением без ограничений (рис. 12, а). Во-первых, были смоделированы повороты в соответствии с реальными условиями и правилами дорожного движения (ПДД). В первом случае (рис.12, в), при отсутствии каких-либо ограничений и ПДД, автомобиль, двигаясь без учета возможности встречного транспорта, мог бы реализовать наикратчайший путь к АЗС. После введения запрещенных манёвров и предписания движения по полосам моделируемая траектория движения изменилась (рис. 12, г), путь удлинился. Несомненно, названные ограничения влияют на построение области обслуживания и их учёт обязателен.
Важность моделирования ареалов сбыта в соответствии с реальными условиями движения поясняет рис. 13. На нем области сбыта в случаях а и б существенно отличаются, и не только по форме. Зелёным цветом показана одноминутная область (время движения автомобиля до АЗС №8), жёлтым – двухминутная, а красным – трёхминутная. На рис. 13,б видно, что в зелёную область вклинилась красная, которая соответствует большему времени движения до АЗС № 8, чем в пределах зелёной области. Это объясняется тем, что на прилегающей к АЗС магистрали организовано двустороннее движение. Более того, между встречными полосами движения находится конструктивно выделенная разделительная полоса. Поэтому автомобили, движущиеся по «высвеченной» полосе, могут попасть на АЗС № 8 только после того как доберутся до первого перекрёстка и совершат разворот. Таким образом, время движения этих автомобилей возрастает, и они не захватываются зелёной временной областью.
Аналогичная ситуация в левой стороне рис. 13,б. Область, прилегающая к магистрали снизу, окрашена в зелёный цвет, в то время как область, прилегающая к этой же магистрали сверху, окрашена в красный цвет. Это также объясняется направлением движения ТС по полосам: по нижней стороне магистрали осуществляется движение ТС в сторону к АЗС, а по верхней – от АЗС.
С учетом этих особенностей выполнено моделирование ареалов выгодного сбыта для условий реальной УДС. Технология работы в основном была прежней, но теперь на первом ее этапе рассматривались не точечные объекты АЗС и эвклидово расстояние по прямой, а построенные в Network Analyst области обслуживания, которые переводились в растр временнoго расстояния.
При рассмотрении растра, смоделированного для реальной УДС (рис. 14), можно заметить, что, например, области автозаправочных станций №№ 19 и 20 не залиты одним цветом, а заполнены неустойчивой штриховкой. Это объясняется наложением базовых стоимостных поверхностей с равной крутизной для близко расположенных АЗС. Однако границу ареала равновыгодности всё же визуально можно определить. Анализируя рис. 14, можно обратить внимание на форму ареалов сбыта: границы многих из них проходят по существующим магистралям УДС, особенно заметно это для ареалов №№ 8, 12, 15, 16.
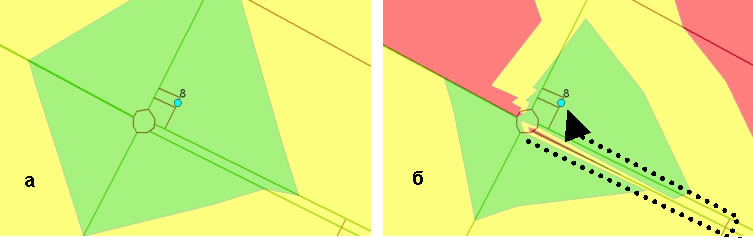
Рис. 13. Ареал сбыта АЗС без учета конкурентов: а) в реальной среде, без ограничений; б) в реальной среде, с ограничениями.
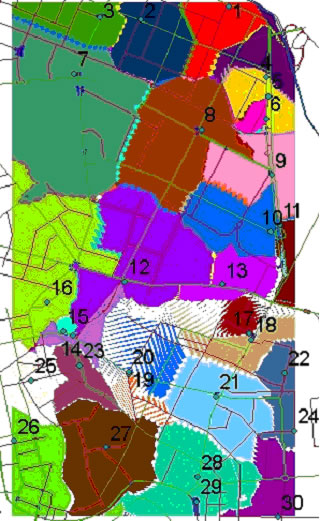
Рис. 14. Растр распределения ареалов для 30 конкурирующих АЗС при учете движения по реальной УДС.
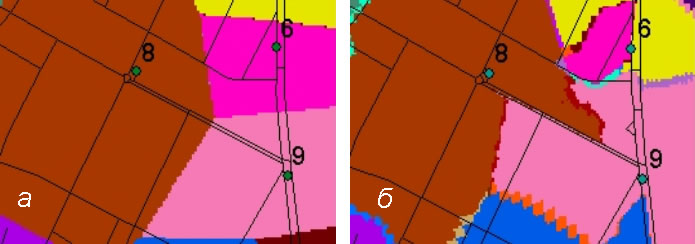
Рис. 15. Растр распределения ареала АЗС с учетом конкурентов: а) на условной УДС, без ограничений; б) на реальной УДС, с ограничениями.
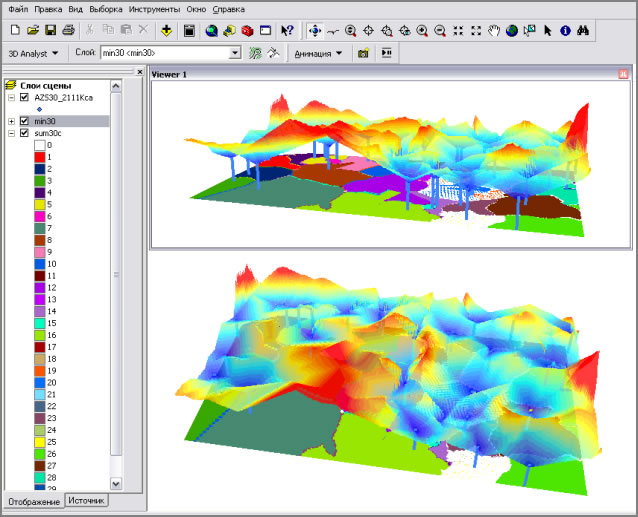
Рис. 16. Стоимостная поверхность (с учетом Сp) для 30-ти конкурирующих АЗС в реальной среде.
В качестве примера детализированного сравнения двух вариантов моделирования представлены растры распределения ареалов одной и той же АЗС № 8, смоделированные без учёта направления движения по полосам и запрещенных манёвров (рис. 15,а) и с учётом таковых (рис. 15,б). Заметно, что растр распределения ареала АЗС № 8 вытянулся вдоль стороны магистрали, движение по которой осуществляется в сторону АЗС. И более того – не только вытянулся вдоль, но и «захватил» именно эту часть дорожного полотна.
Результат 3D-моделирования растра распределения ареалов и стоимостной поверхности для 30-ти конкурирующих АЗС представлен на рис. 16. Плоскость с ареалами выгодного сбыта находится на высоте 18 руб./литр. Производственная цена Cp и транспортный тариф Ct не изменились (в сравнении с рис. 11). Но подключение и учёт реальной дорожной ситуации с помощью инструментария Network Analyst позволили получить иную картину.
Модель дистрибьюторской сети мегаполиса, региона может состоять из нескольких сот пересекающихся “конусов прибыли” (а также дохода), образуя единую “поверхность общей прибыли” (а также “поверхность общего дохода”) – например, 300 АЗС в Петербурге [5]. «Поверхность общего дохода» характеризует выручку от продаж всего дистрибьютерского комплекса, она отражает общую сумму средств, перешедших от совокупного потребителя к совокупному поставщику. Относительно топливораспределения, например, в мегаполисе далее интересны две задачи. Первая – необходимость минимизации общего дохода совокупного поставщика топлива при условии сохранения объема транспортных услуг городу (с этим доходом коррелирует и общий расход топлива, и объем вредных выбросов в атмосферу). Вторая задача – макрологистическая гармонизация (выравнивание) участников рынка топливообеспечивающих услуг. Решению этих задач и принятию решений на региональном уровне будет способствовать визуализация поведения «поверхностей дохода». А это может обеспечить только современная ГИС.
Расчет общего годового дохода 30-ти АЗС Калининского района
Был проведен анализ долевого распределения 150 тыс. автомобилей, отнесенных к Калининскому району, по его 9-ти микрорайонам, существенно отличающимся по характеру использования АТС. По его результатам построен растр плотности заполнения микрорайонов автомобилями. На рис. 17 отображены 4 слоя: а) растр плотности заполнения микрорайонов автомобилямиP, авт./м2; б)растр (идеальный) общей стоимости 1 литра топлива C = Cp + Ct, руб./литр; в) растр годового расхода топлива одним автомобилем Q, литр/(авт.*год), в данном исследовании принято значение Q=1000; г) растр годовых затрат по топливообеспечению 1м2 моторизованной территории PQC, руб./(м2* год) – получаемый локальным перемножением первых трех растров(см. рис. 18).

Рис. 17. Растры, отображающие компоненты модели формирования затрат на топливообеспечение работы автотранспорта в городском районе.
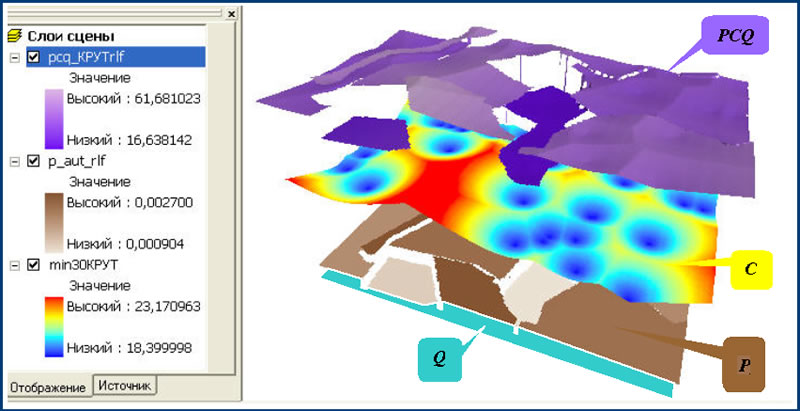
Рис. 18. Представление формирования годовых затрат PCQ по топливообеспечению 1 м2 моторизованной территории в ArcScene.
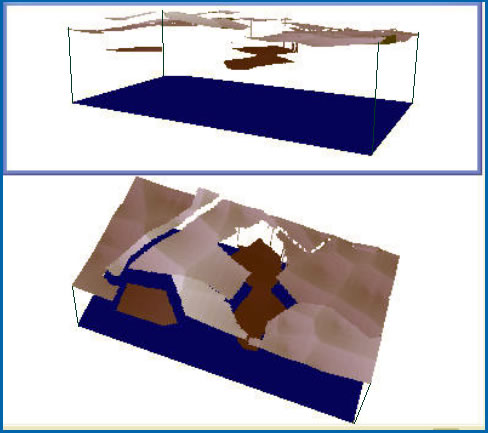
Рис. 19. Формирование объемного образа суммарных затрат по топливообеспечению района.
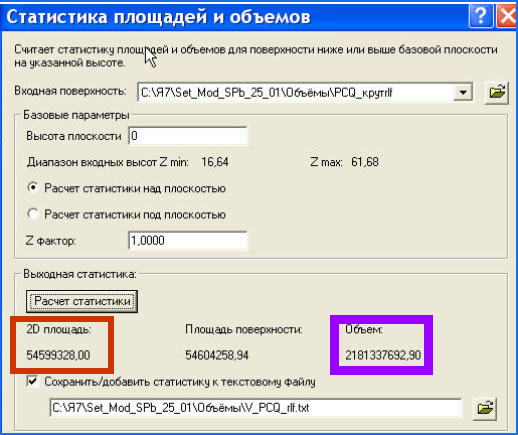
Рис. 20. Результат вычислений расходов на топливообеспечение в среде 3D Analyst.
Объем фигуры под поверхностью PQC до нулевой плоскости (рис. 19), соответствующий интегралу (4), дает значение суммарных годовых затрат по топливообеспечению автотранспорта района. Также средствами модуля 3D Analyst (рис. 20) определено, что на топливообеспечение годовой работы автотранспорта Калининского района площадью 54,6 км2 расходуется 2,18 млрд. руб.
Заключение
Надеемся, мы достаточно наглядно показали широкие возможности применения современных ГИС в решении задач транспортной логистики. Конечно, для дополнительного аналитического обоснования и более полного решения затронутых в статье задач желательно использовать и ряд методов, не входящих в стандартную функциональность современных ГИС. К ним, например, можно отнести: методы символьной алгебры (реализованы в специализированных математических пакетах); расширенную палитру оптимизационных методов, в том числе многокритериальных; развитые модели массового обслуживания, транспортных потоков и другие. Их комплексное использование и интеграция с ГИС позволят существенно повысить самодостаточность совокупности инструментальных средств для решения большого спектра задач в транспортной отрасли.
Литература
1. Котиков Ю.Г., Ложкин В.Н. Транспортная энергетика. М.:, «Академия», 2006, 280 с.
2.Котиков Ю. Г., Маврина А. Ю., Александров Ю.С. Определение границ рынка сбыта при наличии конкурентов. В сб. Логистика: современные тенденции развития: III Международная научно-практическая конференция 22, 23 апреля 2004 г. – СПб.: СПбГИЭУ, 2004. – сс. 142–149.
3. Котиков Ю. Г., Маврина А. Ю.Пространственный анализ рынка сбыта конкурентов, выносящих склады, с использованием визуализации. Ж. «Логистика сегодня», №3, 2004. – сс. 10–16.
4. Котиков Ю. Г., Маврина А. Ю. Использование средств визуализации при исследовании рынка сбыта. Вестник КГТУ. Выпуск 35: «Технология и организация перевозок, управление и безопасность на транспорте». Красноярск, КГТУ, 2004, сс. 98–104.
5. Котиков Ю.Г., Чудаков Р.С. Топливозаправочный комплекс Санкт-Петербурга как объект геосетевого анализа. Сб. докладов 62-ой научной конференции СПбГАСУ, СПб, 2005, сс.94–96.