Никифоров И.А., Заведующий лабораторией геоинформационных технологий Оренбургского госуниверситета, e-mail: ianikiforov@rambler.ru, web: www.osu.ru/sites/gis
Abstract. This article discusses the use of polygonal objects from ArcObjects tools for sophisticated applications. Special attention is given feedback between polygons during their dynamic generation and problems of equal-area planar partition.
В статье рассматриваются вопросы использования полигональных объектов инструментария ArcObjects для решения нетривиальных прикладных задач. Особое внимание уделяется организации обратной связи между полигонами при их динамической генерации и равноплощадным планарным разбиениям.
Необыкновенная функциональность ArcGIS 9 во многом определяется библиотеками ArcObjects, созданными с использованием технологий Microsoft Component Object Model (COM). Среди многих тысяч составляющих их объектов возможно наиболее сложными в геометрическом отношении являются полигоны, которые представляют собой произвольное число областей с замкнутыми границами.
В среде ArcGIS полигоны могут быть составными, то есть поддерживается логическое единство объекта, сложенного из произвольного числа даже несмежных фрагментов. Поскольку на их пространственное размещение не накладывается особых ограничений, это свойство может быть использовано для автоматизации широкого круга прикладных задач, решение которых обычно требует «ручного» вмешательства. Как правило, такие задачи предполагают организацию обратной связи между полигональными объектами при их динамической генерации.
В качестве примера далее приводится описание двух алгоритмов, эксплуатирующих неявные следствия весьма глубоких полигональных концепций, реализованных в ArcGIS 9. Один из них предназначен для генерации непересекающихся между собой, а также с самим полигоном, наименований его вершин, а другой – для разбиения полигона на участки равной площади.
Умные подписи
Предположим, что непересекающиеся подписи должны размещаться только с одной стороны подписываемой фигуры, например, снаружи. Подобные требования обычны при оформлении документации с планами земельных участков, количество которых может измеряться многими сотнями.
В основе метода лежит идея минимизации площади пересечений составного полигона, состоящего из собственно подписываемой области (участка) и прямоугольных оболочек (конвертов), описанных около каждой подписи.
Наложим такой конверт на полигон так, чтобы его центр совпадал с подписываемой вершиной. Тогда, при перемещении конверта на некоторую дискретную дистанцию, общая площадь пересечения задействованных в этом процессе фигур будет убывать при движении конверта к периферии участка и, напротив, возрастать при движении его к центру (рис. 1).
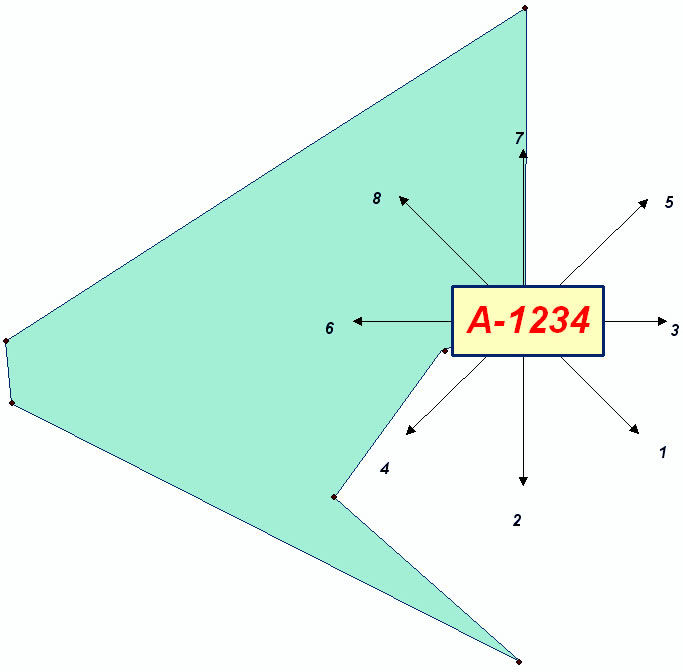
Рис. 1. Роза перемещений оболочки очередной подписи вершины полигона.
В самом деле, если оболочка надписи «А-1234», показанная на рис. 1, будет двигаться по направлениям 5, 4, 3, 2 и 1, площадь наложения её на участок должна сокращаться.
Очевидно, сокращение этой площади в каждом из перечисленных направлений зависит от формы участка, но оптимальная стратегия перемещения надписи требует движения по вектору, для которого зафиксирована минимальная (из всех 8-ми случаев) площадь наложения.
Это действие должно повторяться до тех пор, пока площадь наложения не станет равной нулю. Такая ситуация означает, что оболочка надписи наконец-то утратила смежность с участком, а сама надпись готова к окончательному размещению!
После этого необходимо:
- добавить очередной конверт к участку, как составную его часть (методы AddGeometry и ConstructUnion);
- приступать к подписи очередной вершины.
Циклическое повторение изложенных выше действий для каждой вершины гарантирует автоматический учёт площадей, занятых участком и оболочками предшествующих надписей. Выражаясь метафорически, очередной конверт будет как бы «отталкиваться» ими.
Для работы программы удобно определить массив из 8-ми элементов, каждая строка которого соответствует определённому направлению сдвига, как показано на рис.1. В массив (назовём его rose()) заносятся площади пересечений составного полигона при перемещении оболочки надписи на заданный шаг в направлении, определяемом номером строки этого массива.
Заполнение массива rose() удобно производить с использованием метода Intersect интерфейса ItopologicalOperator. При этом возвращается полигон пересечения, на который можно организовать ссылку объектом Area. Если допустить, что он объявлен как pArea, то площадь пересечения легко определить через свойство pArea.area.
После заполнения массива rose() его надо отсортировать по возрастанию и перенумеровать, чтобы двигаться в первом направлении. Для повышения эффективности уже после первого сдвига можно не проверять направление №8 (рис. 1), поскольку оно было предыдущим, а значит забраковано.
Предлагаемый подход даёт возможность обрабатывать вершины полигонов с очень сложным периметром за счёт автоматической миграции надписей (рис. 2). По сути дела, имитируется технология «ручной» маркировки вершин, которая будет успешна до тех пор, пока имеется достаточное для подписи картографическое пространство.
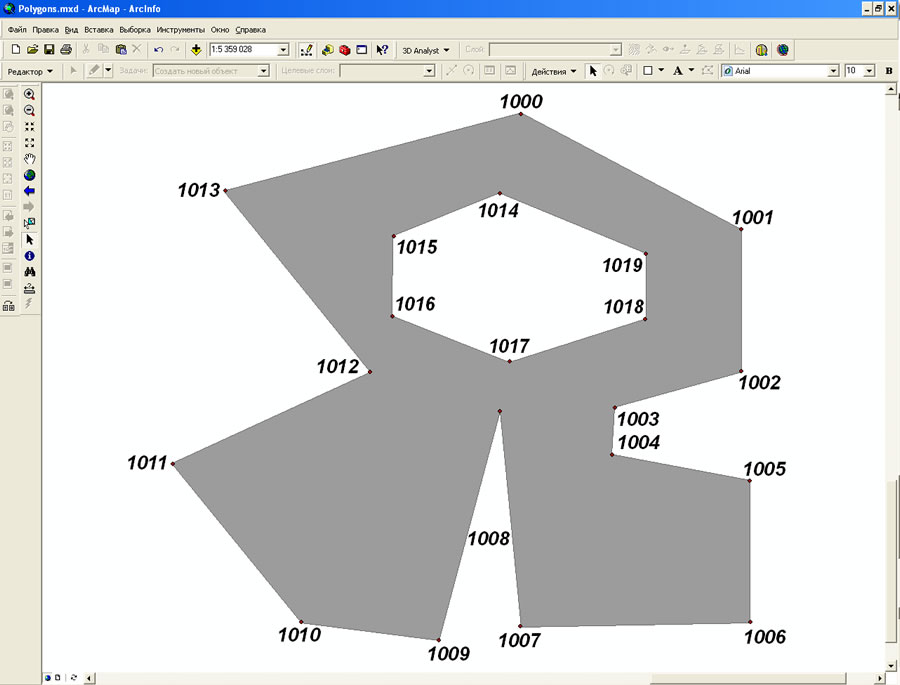
Рис. 2. Пример автоматической подписи вершин полигона.
Равноплощадные разбиения
Весьма актуальной проблемой, связанной с вопросами землеустройства, является разбиение многоугольных участков на фрагменты равной площади. Среди множества подходов к решению подобных задач интересны те, которые сводятся к поиску участков, обладающих некоторыми заранее определёнными свойствами. Другими словами, предполагается, что удовлетворяющие этим требованиям участки (в нашем случае – равноплощадные) уже существуют и имеют свои границы, но они скрыты от непосредственного наблюдения.
К рассмотрению предлагается программно реализованный алгоритм так называемой недетерминированной геометризации. Его название означает, что морфология составляющих полигон мозаичных фрагментов неизвестна заранее и определяется способом их вычленения из сплошной области, последовательно разрезаемой секущими плоскостями. Этот процесс продолжается до тех пор, пока формируемый элемент не достигнет заданной площади.
Работоспособный дихотомический алгоритм для выпуклых фигур состоит в делении исходного полигона на два фрагмента – или равных между собой, или различающихся по площади с точностью до одной доли деления. Для реализации такого подхода была разработана управляющая структура данных, именуемая деревом кратных площадей (ДКП). Иллюстрация работы ДКП в случае деления полигона на 7 равных частей приводится на рис. 3
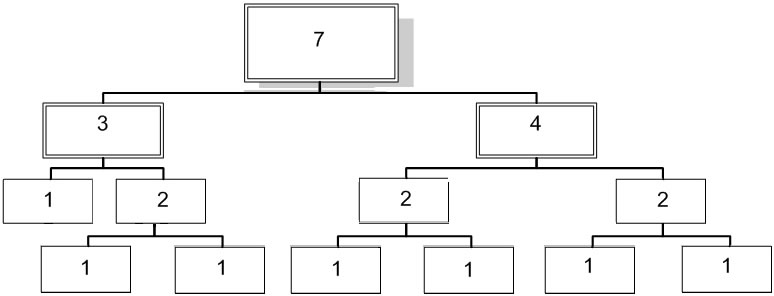
Рис. 3. Дерево кратных площадей.
При делении территории на чётное число участков исходный полигон делится на 2 равные части. Затем каждая часть в свою очередь подвергается делению.
Если же площадь делится на нечётное число участков, то из неё выделяется чётная компонента и остаток. Чётная компонента делится по чётному алгоритму деления, а из остатка в свою очередь выделяются чётная и нечётная части. Как только каждая из компонент превратится в единицу, деление прекращается, что означает завершение поиска элементарного фрагмента.
Во время обхода ДВК происходит:
- Чтение из ДВК площади (S) очередного высекаемого фрагмента.
- Вычисление продольной линии симметрии разбиваемого полигонального фрагмента. В этом качестве используется линейный тренд через вершины рассекаемого полигона.
- Расчёт секущей плоскости, нормальной к оси симметрии, отсекающей от текущего фрагмента осколок площадью S. Она подбирается бинарным поиском через циклическую проверку уже известного нам свойства area. Такой подход позволяет избежать слишком вытянутых и узких отсекаемых фрагментов.
- Если сечение последнее, то – запись полигонального объекта в базу геоданных и рекурсивный возврат к пункту 1.
Результаты работы данного алгоритма представлены на рис. 4.
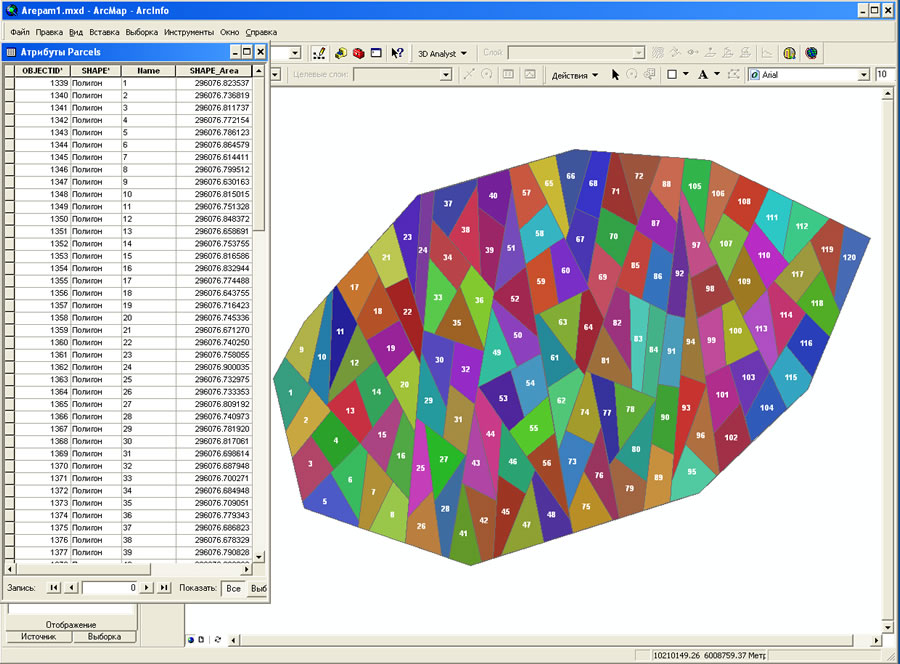
Рис. 4. Разбиение участка на 120 равных по площади частей.
В поле Shape_Area атрибутивной таблицы приведены площади каждого элемента разбиения. Крайне незначительные отличия в них обусловлены задаваемым пределом точности двоичного поиска.
Если исходный полигон не является выпуклым, то необходима предобработка, состоящая в разбиении его на выпуклые доли с площадями кратными площади минимального элемента деления. После этого они могут подаваться на вход основного дихотомического алгоритма, описанного выше.
Таким образом, программный инструментарий ArcGIS 9 предоставляет чрезвычайно широкие возможности алгоритмизации любых идей геометризации пространства. Они ограничиваются только диапазоном нашего воображения и любознательности.
