Имангалин А.Ф., компания SmartLoc, г. Москва, e-mail: info@smartloc.ru, Web: smartloc.ru
Data Quality in Geomarketing Researches
 Применение геоинформационных технологий в геомаркетинге повышает качество и эффективность этих исследований на порядок. Но для полноценного использования набора аналитических инструментов, предоставляемого современными ГИС, нужны различные пространственные данные. Их сбор и формирование соответствующих баз данных может занять значительную часть времени исследования. В связи с этим встает вопрос о путях оптимизации этого процесса и выборе оптимального соотношения между качеством и объемом используемых данных и качеством итогового исследования. В данной статье мы постарались отразить наше видение и опыт решения такого рода задач.
Применение геоинформационных технологий в геомаркетинге повышает качество и эффективность этих исследований на порядок. Но для полноценного использования набора аналитических инструментов, предоставляемого современными ГИС, нужны различные пространственные данные. Их сбор и формирование соответствующих баз данных может занять значительную часть времени исследования. В связи с этим встает вопрос о путях оптимизации этого процесса и выборе оптимального соотношения между качеством и объемом используемых данных и качеством итогового исследования. В данной статье мы постарались отразить наше видение и опыт решения такого рода задач.
Качество данных является одним из ключевых показателей, влияющих на достоверность любого исследования. В данной статье под «качеством» мы будем подразумевать полноту и точность исходной информации.
При создании любой модели необходимо учитывать, какая информация в ней используется и какие ограничения заложены в модели. Пространственные модели взаимодействия, например Хаффа, – не исключение. Одно из ключевых их свойств – это замкнутость изучаемой системы, где основной задачей модели является распределение потенциального покупательского спроса между объектами на определенном локальном рынке. Так, например, увеличение торговой площади увеличивает атрактивность объекта, что влияет на увеличение потенциальной его аудитории, но это влияние нелинейное; в то же время при изменении значений рассматриваемых параметров результаты могут быть не тривиальны. А с увеличением числа изучаемых параметров и количества объектов в модели анализ взаимодействия сильно усложняется.
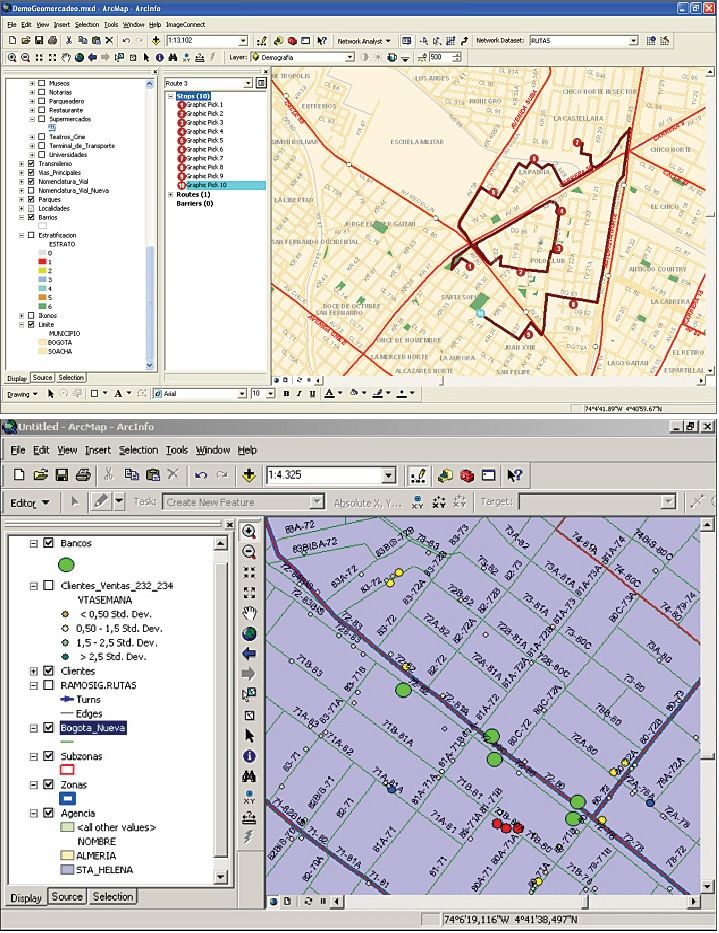
Анализ особенностей взаимодействия с помощью модели зависит от ее охвата. Так, в случае 2-х торговых объектов и 3-х рынков сбыта, изучаемая матрица расстояний составит 2*3 = 6 маршрутов. А когда объектом изучения является город-миллионник, где число торговых точек, например, магазинов продуктов питания, составляется от 400-600 объектов, а число жилых строений (минимальная единица локального рынка) порядка 15-20 тысяч, то изучаемая матрица корреспонденции составит более 10 млн. записей. Такой массив данных тяжело обрабатывать, не говоря уже о различных вариантах сценарного анализа, где изменение вариантов размещения, размеров объекта, потенциальных параметров взаимодействия может достигать в сумме 20-30 итераций. Все это требует значительных ресурсов: как на создание большого массива данных, так и на его обработку. Для проведения такого рода исследований широко используется набор инструментов сетевого анализа модуля Network Analyst, входящий в состав программного ГИС-обеспечения Esri ArcGIS. Данный модуль позволяет провести анализ городской среды с использованием большого объема данных, предлагает развитый функционал и множество настроек.
Исследователи понимают, что чем точнее исходные данные, тем, как правило, лучше результат анализа. В то же время при решении бизнес-задач важен такой атрибут как эффективность, который отражает число ресурсов, затраченных на получение определенного результата. Для получения точного результата требуется довольно много ресурсов в то время, когда они постоянно ограничены. В связи с этим встают вопросы: «Что делать?» и «Какие методы применять?» – особенно в сложный существующий период, когда, с одной стороны, необходимо уменьшать издержки, а с другой – не ухудшить качество.
Здесь необходимо вспомнить про несколько важных принципов:
- Первый – закон Паретто, который гласит, что 20% усилий дает 80% результата, а остальные 80% усилий – лишь 20% результата. Это не жесткое правило, основная его суть в том, что большая часть результатов достигается минимальными усилиями.
- Второй – использование численных методов, например, метода Монте-Карло, суть которого заключается в получении результата с определённой точностью. Хорошим примером для понимания этого метода служит задача по определению площади произвольного круга в квадрате, где мы можем измерить площадь круга точно, или определить его с некой долей точности. Для этого необходимо случайным образом выбрать точки в этом квадрате, определить столько точек попало в круг, а сколько – нет, и далее можно понять какую долю площадь круга занимает от площади квадрата, которая нам известна. Чем больше точек мы изначально выберем, тем точнее определим площадь круга. Тот же принцип действует при проведении социологических опросов.
Для анализа влияния исходной информации на результаты моделирования было решено провести локальное геомаркетинговое исследование на примере одного города и объектов в нем. В качестве исследуемого города взят Ногинск (Московская область). Используемый метод – модель Хаффа, параметры атрактивности и влияния на расстояние имеют степень 2. Информация о рынках сбыта делится на 4 типа с атрибутами численности населения в каждом типе, данные приведены в таблице 1.
Табл. 1. Данные для проведения моделирования.
| Тип данных о потребителях | Число объектов |
| Данные по всем жилым строениям | 5460 |
| Данные по всем жилым высокоэтажным строениям, частный сектор в виде сетки с шагом 100 метров | 1665 |
| Регулярная сетка c шагом 500 метров на территорию жилой застройки | 129 |
| Микрорайоны | 7 |
Важно отметить, что данные по населению в регулярной сетке с шагом 500 метров и информация по выделенным микрорайонам имеют агрегированный характер, где в качестве исходной информации использованы данные по всем жилым строениям.
В качестве графа использовались 2 типа данных:
- подробный дорожный граф со скоростным режимом и атрибутами односторонности;
- генерализованный граф со скоростным режимом, без атрибута односторонности.
Торговыми объектами для проведения анализа выступало 7 точек (рис. 1), три из которых являются ключевыми. На примере этих объектов были произведены расчеты, локации имеют следующую типологию:
- 1-я точка – объект на периферии, расположен вдоль крупной объездной магистрали;
- 2-я точка – расположена в центральной части города возле крупного жилого массива, сформированного многоэтажными домами;
- 3-я точка – объект расположен на полупериферии в крупном частном секторе.
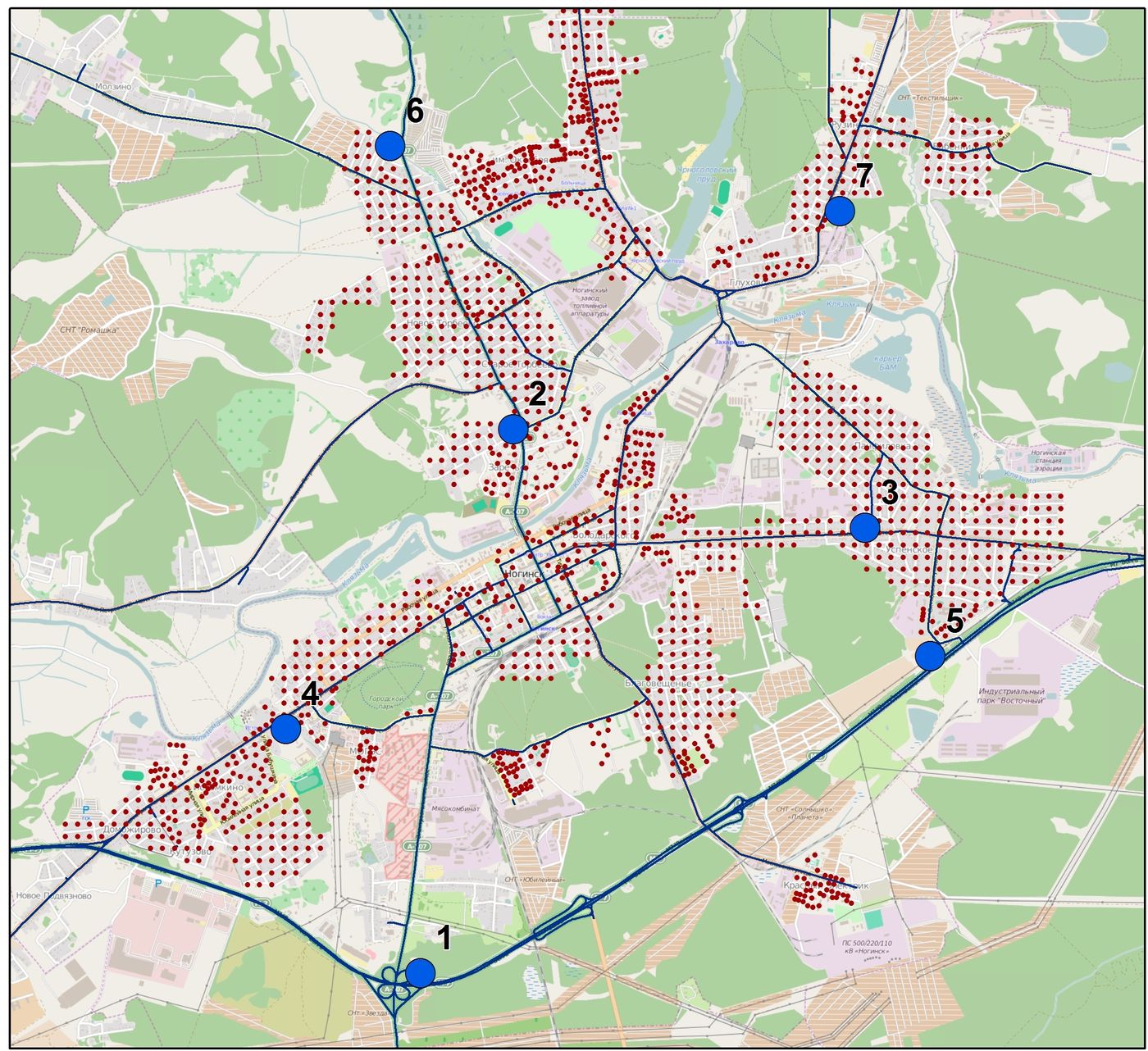
Схема размещения торговых объектов и жилых строений, где частный сектор представлен в виде регулярной сети, генерализованный дорожный граф.
Было проанализировано 2 сценария:
- все объекты – гипермаркеты с зоной обслуживания 20 мин. транспортной доступности;
- все объекты – супермаркеты с зоной обслуживания 5 мин. транспортной доступности.
Эталонными значениями, с которыми сравнивались полученные результаты, являются показатели моделирования с использованием максимально точных данных.
Результаты исследования с 48 итерациями анализа отражены в таблице 2, их комбинации основаны на 4-х типах данных о потребителях, 2-х видах дорожного графа, 2-х типах торговых объектов и трех изучаемых локациях. Таблица показывает, как изменяются значения моделирования (расчет численности потенциальных клиентов по модели Хаффа) от эталонных значений в зависимости от изменения типов используемых исходных данных.
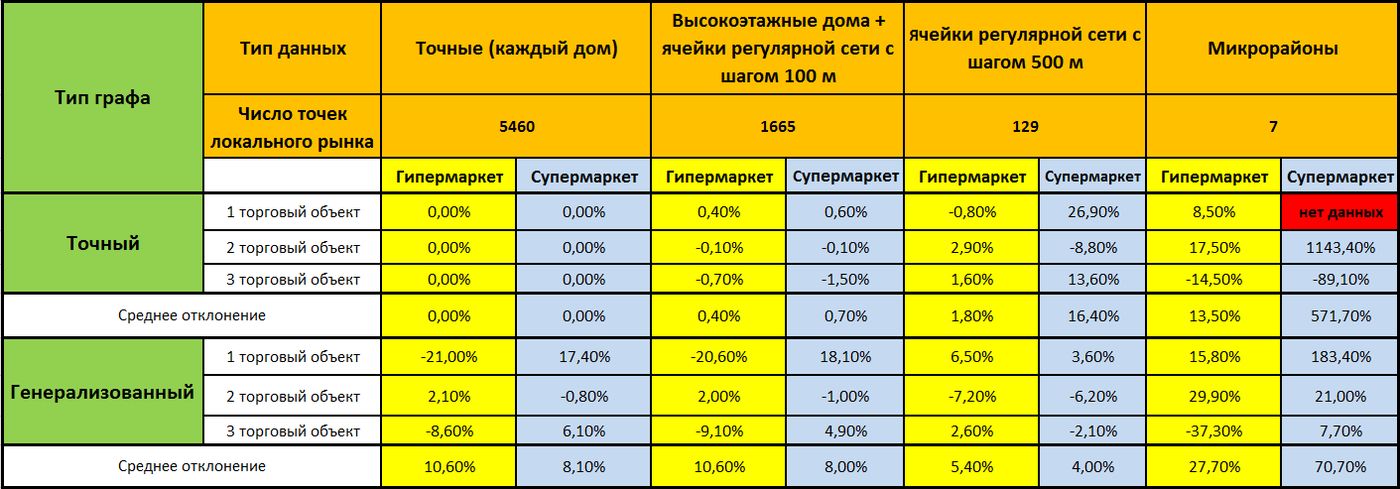
Табл. 2. Сводные результаты геомаркетингового исследования.
При анализе таблицы можно отметить, что:
- при уменьшении объема выборки данных на 69,5% точность моделирования падает максимум на 1,5%, в среднем по 3 точкам для супермаркетов – 0,7%, для гипермаркетов – 0,4%;
- при уменьшении объема выборки данных на 97,6% точность падает максимум на 27%. Среднее значение для супермаркетов 16,4%, для гипермаркетов – 1,8%;
- при анализе 7 районов – данные не подходят для изучения супермаркетов, результаты модели по гипермаркетам будут варьироваться от -14% до +17,5%.
Если мы будем рассчитывать матрицу корреспонденции на основе генерализированного графа, то показатели выделяются рядом особенностей. Неточный автомобильный граф сильнее всего влияет на результаты гипермаркетов, особенно на локации, расположенные на периферии вдоль крупной магистрали. Следует отметить, что при использовании неточного графа необходимо использовать данные по регулярной сетке, в таком случае результат будет наиболее точным.
Основные выводы по статье:
- Необходимый минимум объема и качества данных для исследования зависит от размера и географии обслуживания изучаемого объекта.
- Объем исходных данных влияет на точность результатов не линейно, а имеет степенную функцию, например, увеличение объема данных на 229% может обеспечить прирост точности на 0,7%.
- Точные значения одних данных в модели девальвируются низкой точностью других, то есть, точность модели лимитирована качеством наихудших входящих данных.
- Наилучшие итоговые результаты моделирования достигаются при одинаковом качестве всех входящих данных, как при низком, так и при высоком их качестве.
- Применение возможностей современных ГИС в геомаркетинге позволяет провести разносторонний анализ городской среды с использованием большого объема данных, кардинально повышает качество и эффективность подобных исследований.